Question

Question is in the picture. find the sum of the arithmetic sequence.

Answer 1

Given:

• First term, a1 = 19

,

• an = 309

,

• number of terms, n = 30

Let's find the sum of the sequence.

To find the sum of an arithmetic sequence, apply the formula:

`S=(n)/(2)(2a+(n-1)d)`

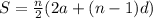
Where d is the common difference.

To find the common difference, d, apply the explicit formula of an arithmetic sequence:

`a_n=a_1+(n-1)d`

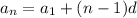
Plug in the values and solve for d:

`\begin{gathered} 309=19+(30-1)d \\ \\ 309=19+(29)d \\ \\ \text{ Subtract 19 from both sides:} \\ 309-19=19-19+29d \\ \\ 290=29d \end{gathered}`

Divide both sides by 29:

`\begin{gathered} (290)/(29)=(29d)/(29) \\ \\ 10=d \\ \\ d=10 \end{gathered}`

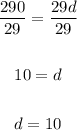
The common difference, d = 10.

Now, plug in values on the sum formula and solve for the sum, S.

We have:

`\begin{gathered} S=(n)/(2)(2a+(n-1)d) \\ \\ S=(30)/(2)(2(19)+(30-1)10) \\ \\ S=15(38+(29)10) \\ \\ S=15(38+290) \\ \\ S=15(328) \end{gathered}`

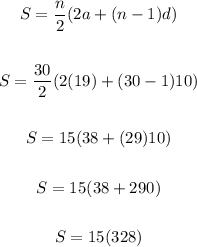
Solving further:

`S=4920`

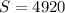
Therefore, the sum of the sequence is 4920.

• ANSWER:

4920