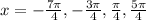1 Answer

Antigp · Answer 1 · 2023-10-19T09:38:53+0000

Question 50.

Given:

cot x = 1

Let's find the solutions of the given equation in the interval: [-2π, 2π].

To solve for the solutions, apply the following steps:

• Step 1.

Take the inverse cotangent of both sides:

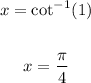
$\begin{gathered} x=\cot ^(-1)(1) \\ \\ x=(\pi)/(4) \end{gathered}$

This function is positive in the first and third quadrants.

• Step 2.

To find the next solution add π to the first solution:

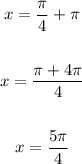
$\begin{gathered} x=(\pi)/(4)+\pi \\ \\ x=(\pi+4\pi)/(4) \\ \\ x=(5\pi)/(4) \end{gathered}$

• Step 3.

Find the period of cotx:

$(\pi)/(|b|)=(\pi)/(|1|)=(\pi)/(1)=\pi$

The period of the cot function will be:

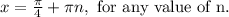
$x=(\pi)/(4)+\pi n,\text{ for any value of n.}$

Substitute -2 for n and solve:

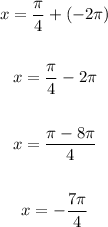
$\begin{gathered} x=(\pi)/(4)+(-2\pi) \\ \\ x=(\pi)/(4)-2\pi \\ \\ x=(\pi-8\pi)/(4) \\ \\ x=-(7\pi)/(4) \end{gathered}$

Substitute -1 for n:

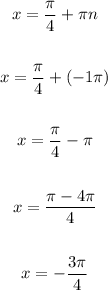
$\begin{gathered} x=(\pi)/(4)+\pi n \\ \\ x=(\pi)/(4)+(-1\pi) \\ \\ x=(\pi)/(4)-\pi \\ \\ x=(\pi-4\pi)/(4) \\ \\ x=-(3\pi)/(4) \end{gathered}$

Substitute 0 for n:

$\begin{gathered} x=(\pi)/(4)+\pi n \\ \\ x=(\pi)/(4)+0 \\ \\ x=(\pi)/(4) \end{gathered}$

Substitute 1 for n:

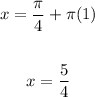
$\begin{gathered} x=(\pi)/(4)+\pi(1) \\ \\ x=(5)/(4) \end{gathered}$

Therefore, the solutions of the equation in the interval are:

$x=-(7\pi)/(4),-(3\pi)/(4),(\pi)/(4),(5\pi)/(4)$

Your comment on this question: