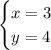Question

Please see the graph for the problem to solve by graphing

Answer 1

The first step to solve the exercise is to graph each equation.

First equation

To graph an equation, we choose some values of x, and we replace them in the equation. Then, we find their corresponding y-values.

For example, if we choose the x-values x = 1 and x = 0, we have:

`\begin{gathered} 2x-2y=-2 \\ 2(1)-2y=-2 \\ 2-2y=-2 \\ \text{ Subtract 2 from both sides} \\ 2-2y-2=-2-2 \\ -2y=-4 \\ \text{ Divide by -2 from both sides} \\ (-2y)/(-2)=(-4)/(-2) \\ y=2 \\ \text{Then, the graph of the equation passes through the point (1,2). } \end{gathered}`
`\begin{gathered} 2x-2y=-2 \\ 2(0)-2y=-2 \\ -2y=-2 \\ \text{ Divide by -2 from both sides} \\ (-2y)/(-2)=(-2)/(-2) \\ y=1 \\ \text{Then, the graph of the equation passes through the point (0,1). } \end{gathered}`

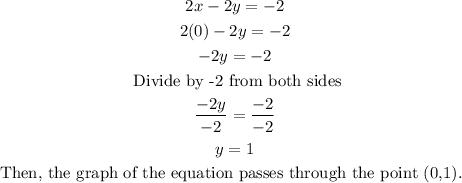
Now, we graph and join the found points.

Second equation

We repeat the previous steps. For example, if we choose the x-values x = 3 and x = -6, we have:

`\begin{gathered} y=-(1)/(3)x+5 \\ y=-(1)/(3)(3)+5 \\ y=-1+5 \\ y=4 \\ \text{Then, the graph of the equation passes through the point (3,4). } \end{gathered}`
`\begin{gathered} y=-(1)/(3)x+5 \\ y=-(1)/(3)(-6)+5 \\ y=2+5 \\ y=7 \\ \text{Then, the graph of the equation passes through the point (-6,7). } \end{gathered}`

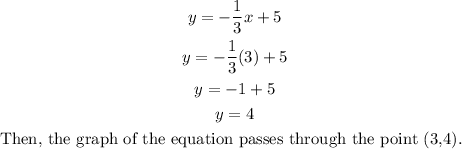
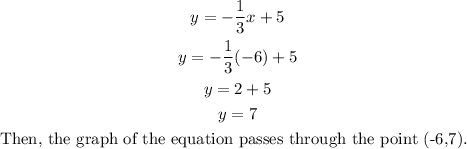
Now, we graph and join the found points.

Finally, the solution to the system will be the point where the two lines intersect.

As we can see, the lines intersect at the point (3,4).

Therefore, the solution of the given system of equation is the ordered pair (3,4) or

`\begin{cases}x=3 \\ y=4\end{cases}`