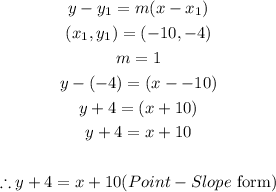Answer:
![undefined]()
We will firstly pick out 2 ordered pairs that lie along the straight line, we have:
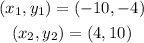
We will proceed to calculate for the slope, we have:
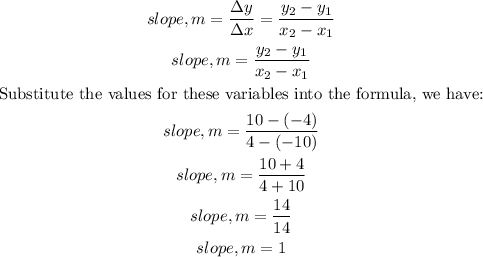
The equation for the general formula of a straight line becomes:
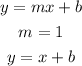
We will proceed using the Point-Slope equation to obtain the equation as shown below: