Question

In the diagram below, AB I AC, CD= CE and m B = 48º.Find m DEB.

Answer 1

In the given triangle the sum of the interior angles of triangle ACB is equal to 180 degrees, therefore, we have the following relationship:

`\angle CAB+\angle ABC+\angle BCA=180`

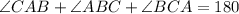
Replacing the values we get:

`90+48+\angle BCA=180`

Solving the operations:

`138+\angle BCA=180`

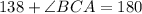
Now we solve for angle BCA by substracting 138 to both sides:

`\begin{gathered} \angle BCA=180-138 \\ \angle BCA=42 \end{gathered}`

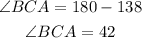
Now, since segments CD and CE are equal, this means that triangle CDE is an isosceles triangle, therefore, its base angles are the same, and we have the following relationship:

`\angle CDE+\angle DEC+\angle ECD=180`

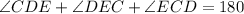
Replacing the known values:

`2\angle DEC+42=180`

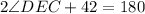
Now we solve for angle DEC by subtracting 42 to both sides:

`\begin{gathered} 2\angle DEC=180-42 \\ 2\angle DEC=138 \end{gathered}`

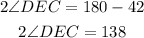
Now we divide both sides by 2:

`\begin{gathered} \angle DEC=(138)/(2) \\ \angle DEC=69 \end{gathered}`

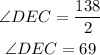
Now, angles DEC and DEB are supplementary, therefore, their sum adds up to 180, therefore, we have:

`\angle DEC+\angle\text{DEB}=180`

Replacing the known angle:

`69+\angle DEB=180`

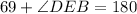
Subtracting 69 to both sides:

`\begin{gathered} \angle DEB=180-69\rbrack \\ \angle DEB=111 \end{gathered}`

Therefore, angle DEB measures 111 degrees.