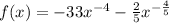Question

Name MA3 - Derivatives (Power Rule) Find the derivative of the following functions. 1. f(x) = 12x² + 4x5 Solution 2. f(x) = 3x + 2x 4 + 23x Solution 3. f(x) = 9x* – 5x + 14,000,605 Solution

Answer 1

1) the fuction is:

`f(x)=12x^2+4x^5`

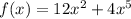
and the derivate will be:

`f^(\prime)(x)=24x+20x^4`

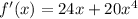
2) The function is:

`f(x)=3x^6+2x^(-4)+23x`

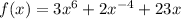
and the derivate:

`f^(\prime)(x)=18x^5-8x^(-5)+23`

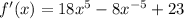
3) the function is:

`f(x)=9x^{(11)/(4)}-5x+14000605`

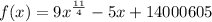
and the derivate will be:

`\begin{gathered} f^(\prime)(x)=(11)/(4)\cdot9x^{(11)/(4)-(4)/(4)}-5+0 \\ f^(\prime)(x)=(99)/(4)x^{(7)/(4)}-5 \end{gathered}`

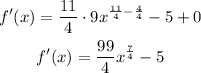
4) the function is:

`f(x)=(4x^6-13x^3-21)/(x^3)`

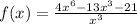
and the derivation will be:

`f^(\prime)(x)=((24x^5-39x^2)x^3-(4x^6-13x^3-21)3x^2)/((x^3)^2)`

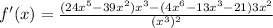
5) the equation is:

`f(x)=(11)/(x^3)-2\sqrt[5]{x}`

first we rewrite the equation so:

`f(x)=11x^(-3)-2x^{(1)/(5)}`

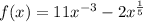
and now we derivate so:

`f(x)=-33x^(-4)-(2)/(5)x^{-(4)/(5)}`