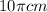The formula to find the arc length if the angle has been measured in degrees is
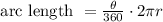
So, for the arc AB, you have
![\begin{gathered} \theta=135\text{\degree} \\ r=5\operatorname{cm} \\ \text{ arc length AB }=\frac{135\text{\degree}}{360\text{\degree}}\cdot2\pi(5cm) \\ \text{ arc length AB }=(135)/(360)\cdot10\pi cm \\ \text{ arc length AB }=(15)/(4)\pi cm \end{gathered}]()
Now, for the arc ACB, you have
![\begin{gathered} \theta=360\text{\degree}-135\text{\degree}=225\text{\degree} \\ r=5\operatorname{cm} \\ \text{ arc length ACB }=\frac{225\text{\degree}}{360\text{\degree}}\cdot2\pi(5cm) \\ \text{ arc length ACB }=(225)/(360)\cdot10\pi cm \\ \text{ arc length ACB }=(25)/(4)\cdot\pi cm \end{gathered}]()
Finally, if you add the arc lengths and leave this sum in terms of π, you have

Therefore, if you add the length of the minor arc AB and the length of the major arc ACB, you get the circumference of the circle, whose measure is