Question

consider the following graph of an exponential function model in the geometric sequence 1 3 9 27 which of the following statements are valid based on the graph? Represents the growth of the factor of the function... select all correct choices

Answer 1

The statements that are valid based on the graph include:

A. When the coordinates (0, 1) and (-1, 1/3) are considered, r = 1/(1/3), which simplifies to 3.

C. When the coordinates (3,27) and (2,9) are considered, r = 27/9, which simplifies to 3.

F. When the coordinates (1,3) and (2,9) are considered, r = 9/3, which simplifies to 3.

In Mathematics and Geometry, the nth term of any geometric sequence can be determined by using the following formula:

`a_n=a_1(r)^(n-1)`

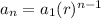
Where:

• 
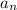  `a_n` is the nth term of any geometric sequence.
• r represents the common ratio.
• 
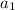  `a_1` represents the first term of any geometric sequence.

Based on the given statements, we would determine the common ratio as follows;

Common ratio, r =
`(r_2)/(r_1)`

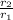
Common ratio, r = 1/(1/3)

Common ratio, r = 3.

For the coordinates (1,3) and (2,9), we have;

Common ratio, r = 9/3

Common ratio, r = 3.

For the coordinates (3,27) and (2,9), we have;

Common ratio, r = 27/9

Common ratio, r = 3.

In this context, we can logically conclude that all of the statements with a common ratio of 1/3 are not valid based on the graph.

Answer 2

we will consider the option one after the other

Option A

When we considered the coordinates (0, 1) and (-1, 1/3)

the growth factor (or the common ratio r is )

Let T_n denotes the nth term

Here, n = 0

`\begin{gathered} r=(T_n)/(T_(n-1)) \\ r=(T_0)/(T_(-1)) \\ r=(1)/(((1)/(3))) \\ r=1/(1)/(3) \\ r=1*(3)/(1) \\ r=3 \end{gathered}`

Correct

Option B

When we considered the coordinates (1, 3) and (2, 9)

Here, n = 2

`\begin{gathered} r=(T_n)/(T_(n-1)) \\ r=(T_2)/(T_1) \\ r=(9)/(3) \\ r=3 \end{gathered}`

False

Option C

When we considered the coordinates (3, 27) and (2, 9)

Here n = 3

`\begin{gathered} r=(T_n)/(T_(n-1)) \\ r=(T_3)/(T_2) \\ r=(27)/(9) \\ r=3 \end{gathered}`

Correct

Option D

When we considered the coordinates (0, 1) and (-1, 1/3)

Here, n = 0

`\begin{gathered} r=(T_n)/(T_(n-1)) \\ r=(T_0)/(T_(-1)) \\ r=(1)/(((1)/(3))) \\ r=1/(1)/(3) \\ r=1*(3)/(1) \\ r=3 \end{gathered}`

False

Option E

When we considered the coordinates (3, 27) and (2, 9)

Here n = 3

`\begin{gathered} r=(T_n)/(T_(n-1)) \\ r=(T_3)/(T_2) \\ r=(27)/(9) \\ r=3 \end{gathered}`

False

Option F

When we considered the coordinates (1, 3) and (2, 9)

Here, n = 2

`\begin{gathered} r=(T_n)/(T_(n-1)) \\ r=(T_2)/(T_1) \\ r=(9)/(3) \\ r=3 \end{gathered}`

Correct