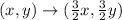Question

Write the rule that was used to transform AABCto AA'B'C' given A(1, 1), B(0, -2);C(4, -1); Ali B(0, -3); and C'(6, –A transformation is described by (x,y) → (-y.x).51. Is this a rotation of 90, 180, or 270 degrees?2. Under this rotation, the image of (5,2) is433. The image of (-4,3) is4. What is the mapping of a rotation of 270degrees?

Answer 1

By definition, Dilations are transformations in which the Image (the figure obtained after the transformation) and the Pre-Image (the original figure), have different sizes, but their shapes are the same.

When the image is larger than the Pre-Image, the scale factor is greater than 1, and when the Image is smaller than the Pre-Image, the scale factor is between 0 and 1.

Therefore, the scale factor is used to change the sizes of the figures.

In this case, you know that the Pre-Image is the triangle ABC, and its Image is the triangle A'B'C'.

Knowing this vertex of the Pre-Image:

`A\mleft(1,1\mright)`

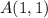
And this vertex of the Image:

`A^(\prime)((3)/(2),(3)/(2))`

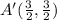
You can identify that A' was obtained by multiplying each coordinate of A by the following scale factor:

`sf=(3)/(2)`

Therefore, you can determine that the Rule for this transformation is:

`(x,y)\rightarrow((3)/(2)x,(3)/(2)y)`

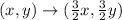
Then, the answer is:

`(x,y)\rightarrow((3)/(2)x,(3)/(2)y)`