Question

A marathon swim follows a triangular course marked with three buoys, A, B, and C. The distance from buoy A to B is 400 meters, B to C is 500 meters, and C to A is 600 meters. What is the largest angle the swimmers must turn between the buoys?

Answer 1

Given:

`\begin{gathered} A-B=400m \\ B-C=500m \\ C-A=600m \end{gathered}`

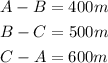
To Determine: The largest angle the swimmers must turn

Solution:

Please note that the largest angle the swimmers must turn is the angle facing the longest side of the triangle

The triangle is as represented below

Using cosine rule, we can solve for the largest angle

`\begin{gathered} b^2=a^2+c^2-2acCosB \\ 2acCosB=a^2+c^2-b^2 \\ CosB=(a^2+c^2-b^2)/(2ac) \end{gathered}`
`\begin{gathered} CosB=(500^2+400^2-600^2)/(2*500*400) \\ CosB=(50000)/(400000) \\ CosB=0.125 \end{gathered}`
`\begin{gathered} B=Cos^(-1)(0.125) \\ B=82.82^0 \\ B\approx83^0 \end{gathered}`

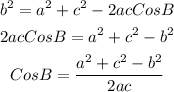
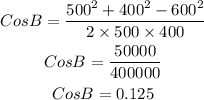
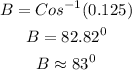
Hence, the largest angle the swimmers must turn between the buoys is approximately 83 degrees