Question

Find the measure of the numbered angles in the rhombus. The diagram is not drawn to scale.

choices;
A. m < 1 = 90, m < 2 = 76, and m < 3 = 14
B. m < 1 = 90, m < 2 = 14, and m < 3 = 83
C. m < 1 = 90, m < 2 = 14, and m < 3 = 76
D. m < 1 = 90, m < 2 = 14, and m < 3 = 14

Answer 1

C.
`m\angle 1=90^(\circ)`,
`m\angle 2=14^(\circ)`, and
`m\angle 3=76^(\circ)`

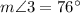
Explanation:

We have been given a rhombus. We are asked to find the angles of our given rhombus.

We know that rhombus is a parallelogram, whose all sides are equal.

Since rhombus is parallelogram, so alternate interior angles will be equal. Therefore, measure of angle 2 is 14 degrees.

The diagonals of rhombus are perpendicular bisector of each other, therefore, measure of angle 1 is 90 degrees.

Since diagonals of rhombus are perpendicular bisector of each other, so they divide rhombus into four congruent triangles.

We can find measure of angle 3 using angle sum property.

`m\angle 3+90^(\circ)+14^(\circ)=180^(\circ)`

`m\angle 3+104^(\circ)=180^(\circ)`

`m\angle 3+104^(\circ)-104^(\circ)=180^(\circ)-104^(\circ)`

`m\angle 3=76^(\circ)`

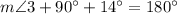
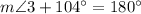
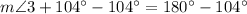
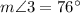
Therefore, measure of angle 3 is 76 degrees and option C is the correct choice.

Answer 2

C. m < 1 = 90, m < 2 = 14, and m < 3 = 76 is the measure of the numbered angles in the rhombus. The diagram is not drawn to scale.