Answer:
The rectangular equivalence is:
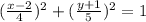
The interval of x is [-2, 6]
Step-by-step explanation:
To find the rectangular equivalence, we want an equation of the form:
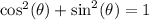
Then, we have the equations:
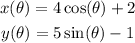
On each equation, we solve for cos and sin:
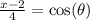
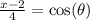
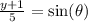
Now we can square both sides:
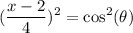
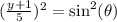
Now we can write:
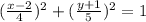
That's the rectangular equivalence of the parametric equations.
Now, to find the interval where x falls under, we have:
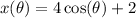
In this function, the value of x depends only on of θ. The maximum value that cos(θ) is 1, when θ = 0
Then, if θ = 0, cos(θ) = 1
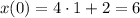
The minimum value of cos(θ) is -1, when θ = π
If θ = π, cos(θ) = -1
Then:

The interval is [-2, 6]