Answer:
Each trigonometric function has two solutions in the interval of its period. As the given cosine function has a period of 24 units and therefore repeats every 24 units, we find the two solutions in the initial range (when n = 0) and add 24n to both of these. Therefore, the variable n represents the number of periods.
Step-by-step explanation:
Given equation:
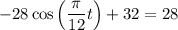
Rearrange the given equation to a function:
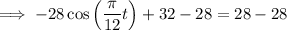
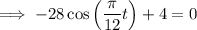
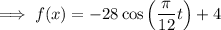
Standard form of a cosine function
![\text{f}(x)=\text{A} \cos \left[\text{B}(x+\text{C})\right]+\text{D}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/4axicsyljaaa74y8to8y.png)
where:
- A = amplitude (height from the midline to the peak).
- 2π/B = period (horizontal distance between consecutive peaks).
- C = phase shift (horizontal shift - positive is to the left).
- D = vertical shift.
Therefore, the period of the given function is:
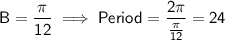
The cosine function is a periodic function. Therefore, the function repeats itself infinitely many times and thus there are an infinite number of solutions.
The period is the length of the shortest interval on the x-axis over which the graph repeats (the horizontal distance between consecutive peaks).
- The period of the given cosine function is 24.
Each trigonometric function has two solutions in the interval of its period.
- The first solution is the principal value.
- The other solution is called the secondary value and lies in a different quadrant.
As the given cosine function has a period of 24 units and therefore repeats every 24 units, we find the two solutions in the initial range and add 24n to both of these. Therefore:
- The variable n represents the number of periods.