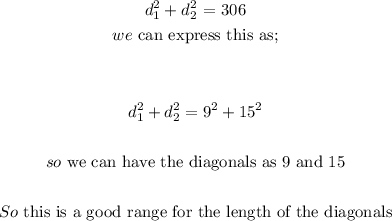Question

Find the range of possible diagonal lengths in a parallelogram with the given side lengths. 4. 3 and 12 5. X and 2x 6. x and x ure

Answer 1

The range of possible diagonal lengths is between 9 and 15

Here, we want to find the range of possible diagonal lengths in a parallelogram with side lengths of 3 and 12

A parallelogram has two diagonals of unequal length

The relationship between the diagonal lengths and the dimensions of the sides are;

`\begin{gathered} d^2_1+d^2_2=2a^2+2b^2 \\ \\ \text{where d}_1,d_2\text{ represents the diagonal lengths, while the a and b represents the length of the sides} \\ \\ we\text{ have;} \\ \\ \text{The sum of the squares of the diagonals as;} \\ 2(3^2+12^2) \\ \\ =\text{ 2(9 + 144)} \\ \\ =2(153)\text{ = 306} \end{gathered}`

so the sum of the diagonals are ;

`\begin{gathered} d^2_1+d^2_2\text{ = 306} \\ we\text{ can express this as;} \\ \\ \\ d^2_1+d^2_2=9^2+15^2 \\ \\ so\text{ we can have the diagonals as 9 and 15} \\ \\ So\text{ this is a good range for the length of the diagonals} \end{gathered}`