Question

The picture shows a barn door.

What is the length of the bar AC?

6 sin 60°

6 cos 60°

Answer 1

SOH, CAH, TOA

sin=oposite/hypotonuse
cos=adjacent/hyptonuse

sin60=CB/6, we want AC

cos60=AC/6
then times 6 both sides
6cos60=ac

answer is 6cos60

Answer 2

Option B is correct.

Length of the bar AC i.e

`AC = 6 \cos 60^(\circ)`

Explanation:

As per the statement:

In right angle triangle ACB

Side AB = 6 feet and
`\angle A = 60^(\circ)`

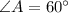
We have to find the length of bar AC:

Using cosine function ratio:

`\cos \theta = \frac{\text{Adjacent Side}}{\text{Hypotenuse side}}`

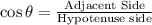
Here,

Adjacent side= AC

Hypotenuse side = AB = 6 feet

`\cos A = \frac{\text{AC}}{\text{AB}}`

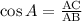
then;

substitute the given values we have;

`\cos 60^(\circ) = \frac{\text{AC}}{6}`

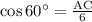
Multiply both sides by 6 we have;

`AC = 6 \cos 60^(\circ)`

Therefore, the length of the bar
`AC = 6 \cos 60^(\circ)`