Question

Two triangles each have adjacent sides of length 120 ft and 180 ft. The first triangle has an angle between the two sides of 40°, while the second triangle has an angle between the two sides of 60°.

What is the approximate difference between the areas of the two triangles?

Answer 1

The difference is around 2410.96 square feet.

Explanation:

To solve this problem, we need to use the definiton of a triangular area but including angles, like the following

`A=(1)/(2)* a * b * sin(C\°)`

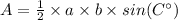
(This formula is used in triangles, where you know two sides and the angle formed).

Where
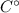`C\°` is the angle of the vertex C, which is equivalent to the difference between the other angles.

So, let's find out the area of each triangle:

`A=(1)/(2)* 120 * 180 * sin(40\°) \approx 6942.11 ft^(2)`

`A=(1)/(2)* 120 * 180 * sin(60\°) \approx 9353.07 ft^(2)`

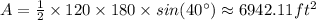
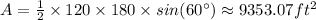
The difference between areas would be

`d=9353.07 - 6942.11 = 2410.96 ft^(2)`

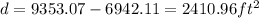
Therefore, the difference is around 2410.96 square feet.

Answer 2

Area of a triangle = 1/2absin C

Difference between the areas of the two triangles = 1/2(120)(180) (sin 60 - sin 40) = 10800(0.2232) = 2411 square feet.