Question

The lengths of two sides of a right triangle are given. Find the length of the third side. Round to the nearest tenth if necessary. legs: 28 in. and 15 in.

A. 37.5 in.
B. 23.6 in.
C. 29.6 in.
D. 31.8 in.

Answer 1

The length of third side is 31.7 inches.

Explanation:

Given :The lengths of two sides of a right triangle are 28 in. and 15 in.

We have to find the length of the third side and choose the correct option.

We can find the third length using Pythagoras theorem

Pythagoras theorem states that in a right angled triangle the sum of square of two sides is equal to the square of third side.

`(H)^2=(B)^2+(P)^2`

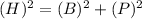
Thus, given two sides are B= 28 in. and P = 15 in.

Thus,

`(H)^2=(28)^2+(15)^2`

`(H)^2=784+225`

`(H)^2=1009`

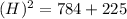
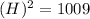
Solve for H , we have,

`H=31.8`

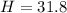
Thus, the length of third side is 31.7 inches.

Answer 2

The answer is D. 31.8 in.

Since this is the right triangle, we can use the Pythagorean theorem:
c² = a² + b²
(c - hypotenuse, a and b - sides)

a = 28 in
b = 15 in

c² = 28² + 15²
c² = 784 + 225
c² = 1009
c = √1009
c = 31.8 in