Question

Solve 3x2 + x + 10 = 0. Round solutions to the nearest hundredth.

x ≈ −2.83 and x ≈ 0.83
No real solutions
x ≈ −2.01 and x ≈ 1.67
x ≈ −1.67 and x ≈ 2.01

Answer 1

No real solutions.

B is correct

Explanation:

Given:
`3x^2+x+10=0`

We are given a quadratic equation and need to solve for x.

Quadratic formula:
`ax^2+bx+c=0`

`x=(-b\pm√(b^2-4ac))/(2a)`

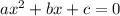
For our equation, a=3, b=1 and c=10

Substitute the value of a, b and c into formula

`x=(-1\pm√(1^2-4\cdot 3\cdot 10))/(2\cdot 3)`

`x=(-1\pm√(-119))/(6)`

Here, Roots are imaginary because number inside the square root is negative.

Hence, No real solutions.

Answer 2

3x2 + x + 10 = 0, delta = 1² - 4.3.10= - 119 <0 so the answer is
b) No real solutions