Question

Tangent Line h(t) = sec t / t @ (Pi, 1/pi)

Answer 1

take derivitive

note
the derivitive of sec(x)=sec(x)tan(x)
so
remember the quotient rule
the derivitive of
`(f(x))/(g(x)) = (f'(x)g(x)-g'(x)f(x))/((g(x))^2)`
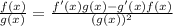
so

the derivitive of
`(sec(t))/(t) = (sec(t)tan(t)t-(1)(sec(t)))/(t^2)`
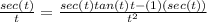
so now evaluate when t=pi
we get
sec(pi)=-1
tan(pi)=0
we get

`((-1)(0)(pi)-(pi)(-1))/(pi^2)= (pi)/(pi^2)= (1)/(pi)`
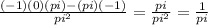
slope=1/pi

use slope point form
for
slope=m and point is (x1,y1)
equation is
y-y1=m(x-x1)
slope is 1/pi
point is (pi,1/pi)

y-1/π=1/π(x-π)
times both sides by π
πy-1=x-π
πy=x-π+1
y=(1/π)x-1+(1/π)
or, alternately
-(1/π)x+y=(1/π)-1
x-πy=π-1