We have the following:
The transformations are as follows:
0. 270 ° rotation clockwise
,
1. Translation of -8 units on the y-axis
,
2. Translation of +20 units on the x-axis
We calculate the area of a triangle knowing that the area is equal to

replacing
b = 15 and h = 4
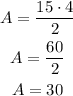
The area is 30 square units
now, since the figure did not have any change in the length of the sides, the area is equal to both the original triangle and the image
0.