Answer
![\operatorname{\lim}_(x\to\pi^(-))f(x)=\infty]()
Vertical asymptote: x = π.

Vertical asymptote: x = 2π.
Step-by-step explanation
Given the graph of the function
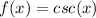
we can find the limit of the function when x approaches π from the left:
Thus:
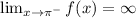
indicating that it has a vertical asymptote at x = π.
Then, we can also find the limit of the function when x approaches 2π from the left:
![\operatorname{\lim}_(x\to(2\pi)^(-))f(x)=-\infty]()
indicating that it has a vertical asymptote at x = 2π.