Question

33. After Jean gave $ 10 to Irene and Irene gave $6 to Todd, Jean had $10 more than Irene and $20 more Todd. Originally, how much more did Jean have than Irene and Todd?A. $14 more than Irene and $16 more than ToddB. $18 more than Irene and $24 more than ToddC. $24 more than Irene and $26 more than ToddD. $24 more than Irene and $36 more than Todd

Answer 1

Let J be how much Jean had initially, I be how much Irene had initially and T be how much Todd had initially.

After Jean gave $10 to Irene, they ende up with:

`\begin{gathered} Jean\colon J-10 \\ Irene\colon I+10 \\ Todd\colon T \end{gathered}`

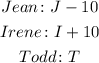
After Irene gave $6 to Tood, they ended up with:

`\begin{gathered} Jean\colon J-10 \\ Irene\colon I+10-6 \\ Todd\colon T+6 \end{gathered}`

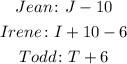
And the question says that, after all this, Jean had $10 more than Irene and 20$ more than Todd, that is:

`\begin{gathered} (J-10)=(I+10-6)+10 \\ (J-10)=(T+6)+20 \end{gathered}`

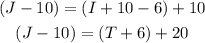
We want to find out how much more Jean had originally than the others, that is:

`\begin{gathered} J-I \\ J-T \end{gathered}`

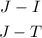
Using the first expression that we got, we can find the first answer:

`\begin{gathered} (J-10)=(I+10-6)+10 \\ J-10=I+4+10 \\ J=I+14+10 \\ J-I=24 \end{gathered}`

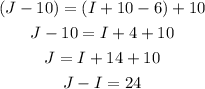
Thus, Jean had $24 more than Irene originally.

Using the second, we can find out the other difference:

`\begin{gathered} (J-10)=(T+6)+20 \\ J-10=T+6+20 \\ J=T+26+10 \\ J-T=36 \end{gathered}`

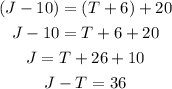
Thus, Jean had $36 more than Todd originally.

The alternative that matches the answer is D.