Question

Standard Solution and Dilution Dry Post-Lab1.) If you add 25 mL of water to 125 mL of 0.15mol/L NaOH solution, what will be the concentration of the diluted solutionRound your answer to three significant digits.

Answer 1

Answer: the concentration of the diluted solution is 0.125 mol/L.

Step-by-step explanation:

The question requires us to calculate the final concentration of a diluted solution prepared by adding 25 mL of water to 125 mL of a 0.15 mol/L NaOH solution.

In a dilution process, the number of moles of a substance does not change, only the volume in which this amount of moles is. Thus, we can write:

`n_(initial)=n_(final)`

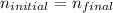
Considering the definition of molarity (also called molar concentration), we can write the following equation to determine the number of moles of a substance:

`\begin{gathered} molarity=\frac{number\text{ of moles of solute \lparen mol\rparen}}{volume\text{ of solution \lparen L\rparen}}\rightarrow C=(n)/(V) \\ \\ n=C* V \end{gathered}`

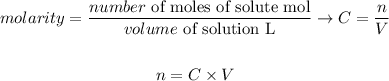
Therefore, we can write the first expression as:

`n_(\imaginaryI n\imaginaryI t\imaginaryI al)=n_(f\imaginaryI nal)\rightarrow C_(initial)* V_(initial)=C_(final)* V_(final)`

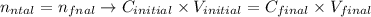
Rearranging this expression, we can calculate the final concentration (Cfinal) that is required by the question.

Remember that the question provided us with the concentration of the initial solution (Cinitial = 0.15 mol/L), the volume taken from the initial solution (Vinitial = 125 mL) and we can calculate the volume of the final solution as a sum of the Vinitial and the volume of water used (Vfinal = 25 + 125 = 150 mL).

Therefore, applying these values to the equation above, we'll have:

`\begin{gathered} \begin{equation*} C_(initial)* V_(initial)=C_(final)* V_(final) \end{equation*} \\ \\ 0.15mol/L*125mL=C_(final)*150mL \\ \\ C_(final)=((0.15mol/L)*(125mL))/((150mL))=0.125mol/L \end{gathered}`

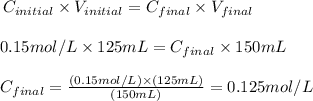
Therefore, the concentration of the diluted solution is 0.125 mol/L.