To determine the arc length, we can use the formula below:
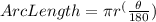
where r = radius and θ = measure of the central angle intercepting the arc.
To help us visualize the question, let's label the diagram with the given information.
As we can see in the diagram, the radius of the circle is 19 units. The measure of the central angle intercepting arc QS is 46°.
Let's use the Arc Length formula stated above and replace the value of r with 19 and θ with 46°.
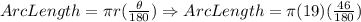
Then, solve.
Divide 46 by 180.
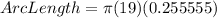
Multiply the result 0.255555 by 19 and the value of π. The result is:
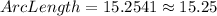
Answer:
The length of Arc QS is approximately 15.25 units.