Question

Find the value of x and y that will ensure the figure is a rectangle.(7y - 2)(5x + 7)(4y +13)X=y=Blank 1:Blank 2:

Answer 1

It's important to know that a rectangle has opposite parallel equal sides, which means that the diagonal is a transversal between the parallels.

We can deduct that the angle 7y-2 and the angle 4y+13 are alternate interior angles because they are between parallels and at different sides of the transversal, which means those angles are equivalent.

`7y-2=4y+13`

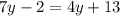
Let's solve for y, first, we subtract 4y from each side.

`\begin{gathered} 7y-4y-2=4y-4y+13 \\ 3y-2=13 \end{gathered}`

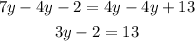
Then, add 2 on each side.

`\begin{gathered} 3y-2+2=13+2 \\ 3y=15 \end{gathered}`

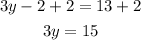
At last, divide both sides by 3.

`\begin{gathered} (3y)/(3)=(15)/(3) \\ y=5 \end{gathered}`

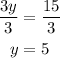
Once we have the value of y, we use it to find x. We know that the angle 5x+7 and the angle 7y-2 are complementary because if the figure is a rectangle, then all its interior angles measure 90°.

`5x+7+7y-2=90`

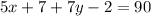
Now we use the value of y and solve for x.

`\begin{gathered} 5x+7+7\cdot5-2=90 \\ 5x+7+35-2=90 \\ 5x+40=90 \end{gathered}`

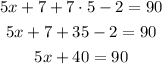
Subtract 40 from each side.

`\begin{gathered} 5x+40-40=90-40 \\ 5x=50 \end{gathered}`

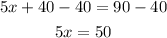
Divide both sides by 5.

`\begin{gathered} (5x)/(5)=(50)/(5) \\ x=10 \end{gathered}`

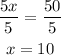
Therefore, the value of x is 10 and the value of y is 5.