Question

If the polar coordinates of the point ( x , y ) are ( r , θ ), determine the polar coordinates for the following points. (Use any variable or symbol stated above as necessary.)

a) -x,y
b)-2x,-2y
c)3x,-3y

I don't understand what they are asking for because i tried the r=sqrt(x^2+y^2) and that theta = tan^-1(y/x) and it was wrong. ...?

Answer 1

⇒Polar Coordinate of point (x,y)=(r,Ф)

The Point (x,y) lies in First Quadrant.

r=Distance from Origin to point (x,y)

`r=√(x^2+y^2)\\\\ \theta=\tan^(-1)(y)/(x)\\\\ \theta=A`

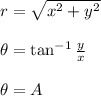
⇒The Point (-x,y) lies in Second Quadrant.

`r=√(x^2+y^2)\\\\ \theta=\tan^(-1)(y)/(-x)\\\\ \theta=\pi-A`

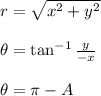
Polar Coordinate of point (-x,y)=(r,π-Ф)

⇒The Point (-2x,-2y) lies in Third Quadrant.

`r=√((-2x)^2+(-2y)^2)\\\\r=√(4x^2+4y^2)\\\\r=2* √(x^2+y^2)\\\\ \theta=\tan^(-1)(-2y)/(-2x)\\\\=\tan^(-1)(y)/(x)\\\\ \theta=\pi+A`

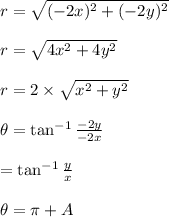
Polar Coordinate of point (-2x,-2y)=(2r,π+Ф)

⇒The Point (3x,-3y) lies in Fourth Quadrant.

`r=√((3x)^2+(-3y)^2)\\\\r=√(9x^2+9y^2)\\\\r=3* √(x^2+y^2)\\\\ \theta=\tan^(-1)(-3y)/(3x)\\\\=\tan^(-1)(-y)/(x)\\\\ \theta=-A`

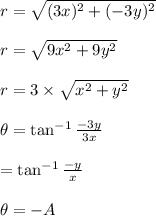
Polar Coordinate of point (3x,-3y)=(3r,-Ф)

Answer 2

Here are the answers to the given values above. Hope these would help you.
Given that the polar coordinates of the point (x,y) are (r, θ ), the polar coordinates of the following would be:
A. The coordinate is just r.
B. The coordinate is just 2r.
C. The coordinate is just 3r.
In addition, to check the angle whether it's counterclockwise or not, so it can be as θ + 180 and so on.