Question

True or false.

The sine of an angle in a right triangle is equal to the ratio of the length of the side adjacent to the angle divided by the length of the hypotenuse. ...?

Answer 1

Answer: The given statement is FALSE.

Step-by-step explanation: We are given to check whether he following statement is true or false :

"The sine of an angle in a right triangle is equal to the ratio of the length of the side adjacent to the angle divided by the length of the hypotenuse. "

Let us consider the right-angled triangle ABC as shown in the attached figure below.

With respect to acute angle C, we can see that

perpendicular, p = AB

base, b = BC

and

hypotenuse, h = AC.

We know that

sine of an angle in a right-angled triangle is equal to the ratio of the perpendicular to the base.

So, we must have

`\sin \angle C=(p)/(h)\\\\\\\Rightarrow \sin \angle C=(AB)/(AC).`

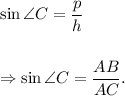
Since AB is the opposite side to angle C, not adjacent, therefore

sine of any angle in a right-angled triangle is the ratio of the length of the OPPOSITE SIDE to length of the hypotenuse.

Thus, the given statement is FALSE.

Answer 2

The answer for the given question above is FALSE. The sine of an angle in a right triangle is equal to the ratio of the length of the side OPPOSITE to the angle divided by the length of the hypotenuse. I hope this answer helps.