The diagram shows statements to prove that both triangles are congruent.
Hence;
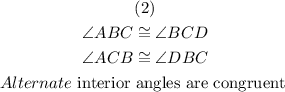
![\begin{gathered} (3) \\ BC\cong BC \\ \operatorname{Re}flexive\text{ property} \end{gathered}]()
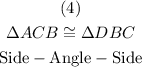
Step 1 showed two sides that are congruent for both triangles
Step 2 showed two angles that are congruent
Step 3 showed two sides that are congruent
Therefore, the triangles are congruent by the side-angle-side theorem