Question

Two airplanes leave Columbus at the same time and fly in opposite directions. one plane travels 70 miles per hour faster than the other plane. after 4 hours they are 4800 miles apart. What is the rate of each plane

Answer 1

The two airplanes travel at different velocities in opposite directions.

We will name the planes "plane 1" and "plane 2" for reference.

One of the planes travels 70 miles per hour faster, so if the velocity or rate of plane 1 is: x, the rate of plane 2 is: x+7.

We see a representation of the situation in the following diagram:

The rate of the planes combined can be found by adding their individual rates:

`x+x+70`

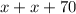
Also, the problem indicates that the planes are at a distance of 4800 miles after 4 hours, so we can use the formula for velocity to find their combined rate:

`\text{Velocity}=(dis\tan ce)/(time)`

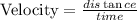
in this case:

`\text{Velocity}=\frac{4800miles}{4\text{hours}}`

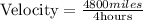
Solving the division we find their combined rate or velocity:

`\text{velocity}=1200\text{ miles per hour}`

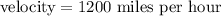
Now we go back to the expression that we got for their combined velocity:

`x+x+70`

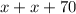
And this expression has to be equal to the combined rate we just found of 1200 miles per hour:

`x+x+70=1200`

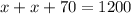
Combining like terms:

`2x+70=1200`

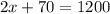
Subtracting 70 to both sides:

`\begin{gathered} 2x=1200-70 \\ 2x=1130 \end{gathered}`

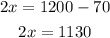
Dividing both sides by 2:

`\begin{gathered} x=(1130)/(2) \\ x=565 \end{gathered}`

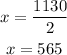
x is equal to 565, which means that Plane 1 is traveling at 565 miles per hour:

And to find the rate of plane 2, we use x+70:

`x+70=565+70=635`

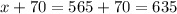
Plane 2 is traveling at 635 miles per hour:

Answer:

the rate of one plane is 565 miles per hour, and the rate of the second plane is 635 miles per hour.