Question

Assume that a sample is used to estimate a population proportion p. Find the 99.9% confidence interval for a sample of size 185 with 118 successes. Enter your answer as a tri-linear inequality using decimals (not percents) accurate to three decimal places.< p < Answer should be obtained without any preliminary rounding. However, the critical value may be rounded to 3 decimal placeMy answer was (4.743,-2.383) but its incorrect

Answer 1

In order to find the confidence interval for a proportion, we can use the formula below:

`CI=p\pm z\cdot\sqrt{(p(1-p))/(n)}`

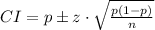
Where p is the probability of success.

For a confidence interval of 99.9%, the critical value is z = 3.291.

Using n = 185 and p = 118/185, we have:

`\begin{gathered} CI=(118)/(185)\pm3.291\cdot\sqrt{((118)/(185)\cdot(67)/(185))/(185)}\\ \\ CI=(118)/(185)\pm3.291\cdot0.035336\\ \\ CI=0.63784\pm0.11629\\ \\ CI=(0.522,0.754) \end{gathered}`

Therefore the answer is 0.522 < p < 0.754.