Question

A customer is comparing the size of pil funnels in a store. The funnels are cone shaped. One funnel has a base with a diameter of 8 in, and a slant height of 12 in. What is the height of the funnel? Round your answer to the nearest hundredth.

Answer 1

Given:

diameter = 8 in

slant height = 12 in

A diagram of the figure is as follows:

Where:

a = slant height = 12 in

R = radius = diameter/2 = 8/2 = 4 in

h = height

From the figure above we can see that a right triangle is formed, so we use the Pythagorean theorem to find the height of the funnel:

`h^2+R^2=a^2`

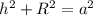
Substitute the values:

`\begin{gathered} h^2+4^2=12^2 \\ h^2+16=144 \end{gathered}`

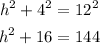
And solve for h:

`\begin{gathered} h^2+16-16=144-16 \\ h^2=128 \\ h=√(128)=11.31 \end{gathered}`

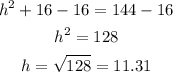
Answer: the height of the funnel is 11.31 in