Question

Group A consists of X students and their total age is 221 and their average age is an integer.When group A is merged with Group B with twice the number of students (the number of students between 30 and 40) average age of B is reduced by 1.What is the original average age of B?

...?

Answer 1

16 years

Explanation:

Given,

Number of students in group A = X,

Sum of their ages = 221,

So, the average age of students in group A =
`\frac{\text{Sum of ages}}{\text{Total students}}`

`=(221)/(X)`

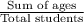
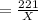
According to the question,

`(221)/(X)=\text{Integer}`

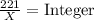
∴ X must be a factor of 221,

∵ 221 = 13 × 17,

Now, If X = 13,

Then the number of students in group B = 26 ( NOT POSSIBLE )

If X = 17,

Then the number of students in group B = 34

Which is between 30 and 40,

Now, Let S be the sum of ages of students in group B,

So, the average age in group B =
`(S)/(34)`

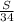
Again according to the question,

`(S+221)/(17+34)=(S)/(34)-1`

`(S+221)/(51)=(S-34)/(34)`

`34S+7514 = 51S - 1734`

`34S - 51S = -1734 - 7514`

`17S = 9248`

`\implies S = 544`

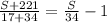
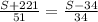
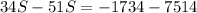
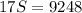
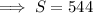
Therefore, the average age of B =
`(544)/(34)` = 16 years.

Answer 2

mean = sum / count

Group A
m = 221 / c
221 = c x m
221 = 17 x 13 (as it is a whole number under 20)

Group B
m = s / 34

(221 + x) / 51 = x /34 - 1

544/ 34 = 16

16