Question

4. Part A A seesaw with the construction shown is being built at a playground. The seating board will be 10 feet long, and the board will make an angle of 30° when it touches the ground. 10feet R Seating Board 300 Central Support Find the height of the central support. Show your work or explain your answer, Round your answer to the nearest tenth of a foot.

Answer 1

Given:

Angle, θ = 30 degrees

Length of board = 10 feet

Let's find the height of the central support.

To find the height of the central support, apply the trigonometric ratio formula for sine.

We have:

`\sin \theta=\frac{\text{opposite}}{\text{hypotenuse}}`

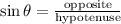
Where:

To find the hypotenuse, since we have a central support, it means the central support divides the seating board into two equal parts.

Thus, we have:

`\text{Hypotenuse}=(10)/(2)=5\text{ fe}et`

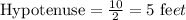
Opposite side is the side opposite the given angle. Here, the side opposite the given angle is the central support.

Let's solve for the opposite side.

To find the height of the central support, we have:

`\begin{gathered} \sin \theta=\frac{\text{opposite}}{\text{hypotenuse}} \\ \\ \sin 30=\frac{\text{opposite}}{5} \\ \\ \text{Multiply both sides by 5:} \\ 5(\sin 30)=\frac{\text{opposite}}{5}\ast5 \\ \\ 5\sin 30=\text{opposite} \\ \\ 5(0.5)=opposite \\ \\ 2.5=\text{opposite} \\ \\ \text{opposite}=2.5\text{ ft} \end{gathered}`

Therefore, the height of the central support is 2.5 feet

ANSWER:

2.5 feet