To determine the radius of the circle using the portion shown in the picture you have to use the formula to calculate the arc length of the segment.
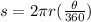
Where
s is the arc length
r is the radius
π is the number pi
θ is the central angle
For the portion of the circle shown in the picture, the arc length is s=15cm and the angle is θ=27º
The first step you have to write the formula in terms of r:
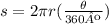
-Divide both sides by 2π

-Multiply both sides of the expression by the reciprocal fraction of (θ/360), which is (360/θ)
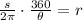
Next, replace the formula with the given arc length and angle and calculate the radius:
![\begin{gathered} r=(s)/(2\pi)\cdot(360)/(\theta) \\ r=(15)/(2pi)\cdot(360)/(27) \\ r=31.8\operatorname{cm} \end{gathered}]()
The radius has a measure of 31.8cm