Question

What is the solution to 3+4e*+1 = 11?X = In 2-1O X=In2+ 11O X=ex=x-2e+ 2OX=e

Answer 1

To solve the expression:

`3+4e^(x+1)=11`

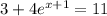
The first step is to leave the exponential term alone on the left side of the equation:

-Pass 3 to the right side by applying the opposite operation to both sides of it:

`\begin{gathered} 3-3+4e^(x+1)=11-3 \\ 4e^(x+1)=8 \end{gathered}`

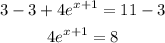
-Divide both sides by 4

`\begin{gathered} (4e^(x+1))/(4)=(8)/(4) \\ e^(x+1)=2 \end{gathered}`

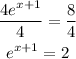
-To take the x-term from the exponent place, apply the natural logarithm to both sides of the expression

`\begin{gathered} \ln (e^(x+1))=\ln 2 \\ x+1=\ln 2^{} \end{gathered}`

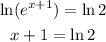
-Finally, pass 1 to the right sides of the expression by applying the opposite operation to both sides of the equal sign:

`\begin{gathered} x+1-1=\ln 2-1 \\ x=\ln (2)-1 \end{gathered}`

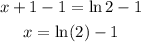
The correct option is the first one.