Question

AB =+atio:22. Little to big ratio:23. Little to bigА.x + 115 B96MMm1212x + 5DHРNProportion to solve for x:Proportion to se for x:Gdt.lvX =X =AC =MN =

Answer 1

Question 22.

Given:

• LQ = 9

,

• QP = 12

,

• LM = 6

• LN = x

Let's solve for x and MN.

Here, both triangles are similar.

To solve for the missing sides, apply the proportionality equation.

We have:

`(LP)/(LQ)=(LM)/(LN)`

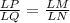
• Where:

LP = LQ + QP = 9 + 12 = 21

• Input values into the equation and solve for x:

`(21)/(9)=(x)/(6)`

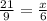
• Cross multiply:

`\begin{gathered} 9x=21\ast6 \\ \\ 9x=126 \end{gathered}`

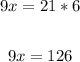
• Divide both sides by 9:

`\begin{gathered} (9x)/(9)=(126)/(9) \\ \\ x=14 \end{gathered}`

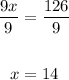
The value of x = 14.

To solve for MN, we have:

LN = LM + MN

MN = LN - LM

MN = 14 - 6

MN = 8

ANSWER:

• Proportion to solve x:

`(21)/(9)=(x)/(6)`

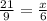
• x = , 14

• MN = , 8