Question

A company that manufactures swimming pools estimates that its profit for selling a particular size is given by the function P(x) = -45x3 + 2500x2 -275,000 where x is the cost of advertising in tens of thousands of dollars. Find the smaller of the two advertising amounts that produce a profit of $800,000. You may use your calculator to do this and round your answer to the nearest whole number. Be sure to label properly.

Answer 1

From the question;

we are given the function

`p(x)=-45x^{3^{}^{}}+2500x^2\text{ - 275,000}`

where

p(x) = profit

x = cost of advertising

we are to find the smallest of the two advertising amounts that produce a profit of $800,000.

this implies

p(x) = $800, 000

Therefore we have

`800,000=-45^3+2500x^2\text{ - 275,000}`

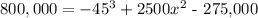
by simplifying the equation we get

`\begin{gathered} 45x^3-2500x^2\text{ + 800,000 + 275,000 = 0} \\ 45x^3-2500x^2\text{ + 1,075,000 = 0} \end{gathered}`

solving the equation using a calculator

we get the values of x to be

`\begin{gathered} x_{1_{}}=-18.0,x_2=42.0_{} \\ \text{and } \\ x_3=\text{ 31.5} \end{gathered}`

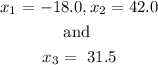
Since cost cannot be negative,

then the real solutions are

`\begin{gathered} x_2\text{ = 42.0 } \\ \text{and } \\ x_3=32.0\text{ ( to the nearest whole number)} \end{gathered}`

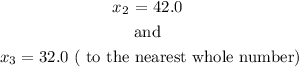
Therefore,

The smaller of the two advertising amounts that produce a profit of $800,000 is

x = 32