Question

All 6 members of a family work. Their hourly wages (in dollars) are the following.37, 38, 39, 40, 39, 11Assuming that these wages constitute an entire population, find the standard deviation of the population. Round your answer to two decimal places.

Answer 1

We have a sample that in fact represents the population.

We have to calculate the standard deviation of this population.

The difference between the standard deviation of a population comparing it to the calculation of the standard deviation of a sample is that we divide by the population side n instead of (n-1).

We have to start by calculating the mean of the population first:

`\begin{gathered} \mu=(1)/(n)\sum ^n_(i=1)\, x_i \\ \mu=(1)/(6)(37+38+39+40+39+11) \\ \mu=(204)/(6) \\ \mu=34 \end{gathered}`

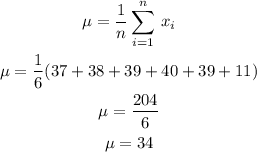
Now, we can calculate the standard deviation as:

`\sigma=\sqrt[]{(1)/(n)\sum^n_(i=1)\, (x_i-\mu)^2}`
`\begin{gathered} \sigma=\sqrt[]{(1)/(6)((37-34)^2+(38-34)^2+(39-34)^2+(40-34)^2+(39-34)^2+(11-34)^2)} \\ \sigma=\sqrt[]{(1)/(6)(3^2+4^2+5^2+6^2+5^2+(-23)^2)} \\ \sigma=\sqrt[]{(1)/(6)(9+16+25+36+25+529)} \\ \sigma=\sqrt[]{(1)/(6)(640)} \\ \sigma\approx\sqrt[]{106.67} \\ \sigma\approx10.33 \end{gathered}`

Answer: the standard deviation of this population is approximately 10.33