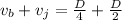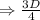Question

It takes Brian four hours to rake the front lawn while his brother John can rake the lawn in two hours. How long will it take them to rake the lawn working together?

Answer 1

4 /3 or 1.33 hours

Step-by-step explanation:

The relationship between raking rate v, the time t and the distance to rake D is given by

`D=vt`

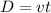
The above can be solved for t to give

`t=(D)/(v)`

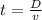
It takes brian 4 hours to rake the front lawn. Therefore,

`D=v_b\cdot4`

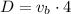
solving for vb gives

`v_b=(D)/(4)`

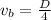
It takes John two hours to take the same lawn. Therefore,

`D=v_j\cdot2`

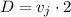
solving for vj gives

`v_j=(D)/(2)`

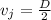
where

v_b = rate at which brian rakes

v_j = rate at which john rakes.

Now, if they both worked together, then their raking rate would be,

`v_b+v_j`

Therefore, the time it takes to rake the same lawn would be

`t=\frac{D}{v_b+v_j_{}}`

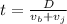
Since we found that v_b = D / 4 and v_j = D /2, the above gives

`v_b+v_j=(D)/(4)+(D)/(2)`
`=(D)/(4)+(2D)/(4)=(3D)/(4)`
`\Rightarrow(3D)/(4)`