Step-by-step explanation
Let's use M for the number of manicure appointments per day and H for the number of haircut appointments per day. We know that a maximum of 50 appointments can be scheduled each day so we have the following inequality:
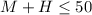
The number of appointments are of course positive numbers so we also have:
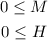
We are told that there are 5 stylist that work 6 hours a day. This means that the total number of hours spent by all the stylist during all the appointments is 5*6=30. The total time spent in hours in manicure appointments is given by (hours per manicure)*M and the time spent in hours in haircut appointments is given by (hours per haircut)*H. We have the length of each type of appointment in minutes so we must convert them into hours. In order to do that we simply need to divide the number of minutes by 60 since there are 60 minutes in an hour:
![\begin{gathered} \text{hours per manicure}\rightarrow(30)/(60)=(1)/(2) \\ \text{hours per haircut}\operatorname{\rightarrow}(50)/(60)=(5)/(6) \end{gathered}]()
Then the total time added from all the appointments can't be greater than 30 hours and is given by the following inequality:
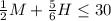
Finally, the profits are given by the sum of the profits generated by haircuts and manicures. The salon makes $12 per manicure and $18 per haircut so the profits from manicures are given by 12M where those from haircut are given by 18H. Then the profits P(M,H) are given by:
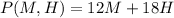
So we basically need to maximize the function above considering that it has some constrains. These constrains are the inequalities that we found before:
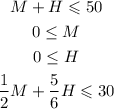
This is a linear programming problem that can be solved using graphs. We first graph the region delimited by the four inequalities above i.e. the region in the (M,H) plane where the four inequalities are met at the same time:
The red, blue, green and orange lines are given by replacing the inequalities symbols with = symbols in the 4 inequalities. The purple shaded region is the region where all these inequalities are met and it's known as the feasible region. The idea behind linear programming is that the pair of values (M,H) that makes the profit function P(M,H) maximum is one of the vertex of the feasible region. Therefore we just need to find the profits for each of the 4 black dots, the biggest value will indicate the solution.
Remember that the profit function is:
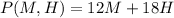
We test the four points:
![\begin{gathered} (M,H)=(0,0)\rightarrow P(0,0)=12\operatorname{*}0+18\operatorname{*}0=0 \\ (M,H)=(0,36)\operatorname{\rightarrow}P(0,36)=12*0+18*36=648 \\ (M,H)=(35,15)\operatorname{\rightarrow}P(35,15)=12*35+18*15=690 \\ (M,H)=(50,0)\operatorname{\rightarrow}P(50,0)=12*50+18*0=600 \end{gathered}]()
So the ordered pair that maximizes the profits is (M,H)=(35,15).
Sketching the graphs by hand
In order to identify the feasible region we first need to graph the 4 constrains given by the inequalities. These are regions delimited by lines since the inequalities are linear therefore we just need to graph those lines. In order to graph a line you just need two of its points.
The equation of the line of the first inequality is given by changing the inequality symbol by a = symbol:
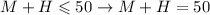
Then we have to find two points that are part of this line. We can re write the equation first:
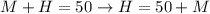
We choose two random M values and we use the equation to find their respective H values. We can use M=0 and M=10:
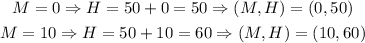
So the line delimiting this inequality is the one passing through (0,50) and (10,60). The region were the inequality is met is that below this line.
For the other inequalities we do the same procedure. We take two values of M and we find their respective H values or the other way around, we take two values of H and we find their respective M values.
Answers
In order to maximize profits 35 appointments must be manicures and 15 must be haircuts.
The maximum profit per day is $690.