we are given that an object begins its motion from the origin at a constant acceleration equal to:
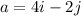
This means that the components in the "x" and "y" direction of the acceleration is:
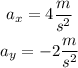
Since this is a motion at constant acceleration this means that the position "x" is given by:
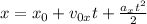
Where:

Since the particle begins at rest from the origin this means that the initial velocity and position are zero:
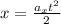
The same can be applied for the y-position and we get:
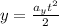
Now, we can determine the path of the object by eliminating the parameter "t" from the equations. To do that we will solve for "t" in the equation for "x". First, we multiply both sides by 2:
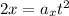
Now, we divide both sides by the acceleration:
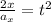
Now, we take the square root to both sides:
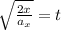
The same procedure is done for the y-position and we get:
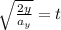
Now, we set both equations equal:
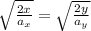
-Now we can cancel out the square roots:
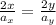
We can cancel out the 2:
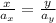
now, we solve for "y" by multiplying both sides by the acceleration in the y-direction:
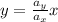
Now, we substitute the values
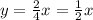
This is the trajectory of the motorboat.
Now, we are given that a fallen branch has uniform velocity and is given by:
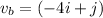
This means that the "x" and "y" components of the velocity are:
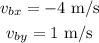
We are also given the initial position:
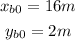
Since the movement is at constant speed this means that the "x" position is given by:
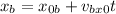
And the "y" position is given by:
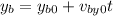
We will determine the equation of the trajectory by eliminating the parameter "t". First, we solve for "t" in the equation of the "x" position. First, we subtract the initial "x" position:
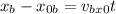
Now, we divide by the initial velocity:
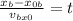
Now, we substitute the known values:
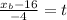
Doing a similar procedure we get the equation of "y":
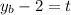
Now, we set them equal:
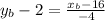
Adding 2 to both sides:
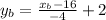
Now, we simplify:
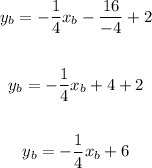
This is the equation of the trajectory of the leaf. Now, we graph both trajectories. We get:
We notice that the trajectories show that the leaf and the boat intercept at the point:
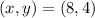
Therefore, the objects collide.
To determine the time we will substitute the value of the x-coordinate if the interception is the formula for the x-position of the boat:
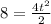
Now, we solve for "t". First, we multiply both sides by 2:
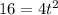
Now, we divide both sides by 4:
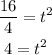
Now, we take the square root to both sides:
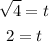
Therefore, the objects intercept after 2 seconds.