Question

Plane A has just 1 ton of fuel left and has requested plane B to refuel it. Plane B has 21 tons of fuel. Fuel transfer happens at the rate of 1 ton per minute. Use this information as you work through the activity and find how long it will take to refuel plane A until both planes have the same amount of fuel. Let x be the time in minutes and y be the amount of fuel in tons. The equation y = x + 1 represents the quantity of fuel with respect to time in plane A, and y = -x + 21 represents the quantity of fuel with respect to time in plane B. For each equation, find two points that satisfy the equation.Graph the equations.

Answer 1

`\begin{gathered} y=x+1 \\ y=x+21 \end{gathered}`

To graph a equation of a line:

1. Find two point on each equation: (x,y)

Give to x or y a value and calculate the value of the other variable.

First equation:

`y=x+1`

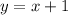
If x is 0

`\begin{gathered} y=0+1 \\ y=1 \end{gathered}`

If y is 0

`\begin{gathered} 0=x+1 \\ -1=x \end{gathered}`

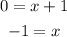
Two points for the first equation: (0,1) and (- 1 , 0)

2. Put the points in the number plane and dfraw a line that cross those points:

Graph for first equation:

------------------

Second equation:

`y=-x+21`

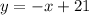
If x=0

`\begin{gathered} y=-0+21 \\ y=21 \end{gathered}`

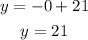
If y=0

`\begin{gathered} 0=-x+21 \\ -21=-x \\ 21=x \end{gathered}`

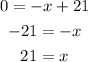
Two points for the second equation: (0,21) and (21,0)

Graph for the system of equation:

The solution for the system of equations is the point when the lines cross each other: (10,11) Then, both planes will have the same amount of fuel after x=10 minutes