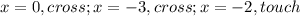Question

For the polynomial function ƒ(x) = x(x + 3)(x + 2)^2, find the zeros. Then determine the multiplicity at each zero and state whether the graph displays the behavior of a touch or a cross at each intercept.x = 0, cross; x = −3, touch; x = −2, touchx = 0, cross; x = −3, cross; x = −2, touchx = 0, touch; x = −3, touch; x = −2, touch x = 0, cross; x = −3, cross; x = −2, cross

Answer 1

Given:

`f(x)=x(x+3)(x+2)^2`

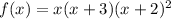
To get the zeros, the zeros exist when f(x) = 0

`\begin{gathered} 0=x(x+3)(x+2)^2 \\ x=0 \\ Multiplicity=1\text{ \lparen odd multiplicity\rparen} \\ \\ \\ x+3=0 \\ Hence,\text{ }x=-3 \\ Multiplicity=1\text{ \lparen odd multiplicity\rparen} \\ \\ \\ (x+2)^2=0 \\ (x+2)(x+2)=0 \\ x=0-2 \\ x=-2\text{ \lparen twice\rparen} \\ Multiplicity=2\text{ \lparen even multiplicity\rparen} \end{gathered}`

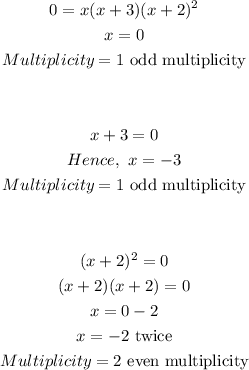
To get the behavior of the graph, the rule below applies;

The graph of a polynomial function will touch the x-axis at zeros with even multiplicities. The graph will cross the x-axis at zeros with odd multiplicities.

The graph of the function showing the x-intercepts and the behavior of the zeros is shown;

Therefore, in conclusion:

`x=0,cross;x=-3,cross;x=-2,touch`