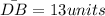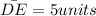Given:
AE=EB=12.
AC=3x-12 and BC=2x+4.
By perpendicular bisector property, we get
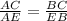
Substitute AE=EB=12, AC=3x-12 and BC=2x+4, we get
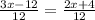
Cancel out the common term, we get
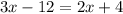
Adding 12 to both sides of the equation, we get
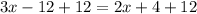
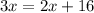
Subtracting 2x from both sides of the equation, we get
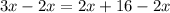
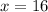
Substitute x=16 in AC=3x-12 , we get
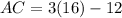
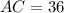
We get AC=36 units.
Given that AD=y+16 and DB=3y+22 and AE=EB=12.
By perpendicular bisector property, we get
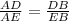
Substitute AD=y+16 and DB=3y+22 and AE=EB=12 in the equation, we get
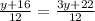
Cancel out the common terms, we get
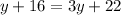
Subtracting 22 from both sides, we get
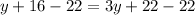

Subtracting y from both sides of the equation, we get
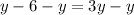
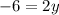
Dividing both sides by 2, we get
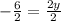
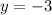
Substitute y=-3 in DB=3y+22, we get
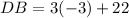

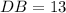
We get DB=13.
Use Pythagorean theorem to find DE.
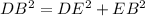
Substitute DB=13 and EB=12 in the equation, we get
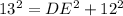
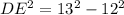
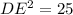
Taking square root on both sides, we get
![DE=\sqrt[]{25}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/idk3lswtyvmrmx4tpg6m.png)
![DE=\sqrt[]{5^2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/3ymwpo8vpyn2jpaeovr9.png)
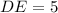
We get DE=5 units.
Hence the answers are