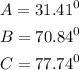Step-by-step explanation
In the question, we are given that the triangular toy bin has three sides 16 inches, 29 inches and 30 inches. To find the respective angles for each side, we will use the cosine rule.
Lets name each side with letters.
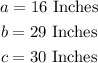
To find the angles we will use the formula below;
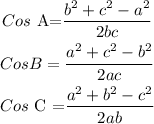
We can then insert the sides to have;
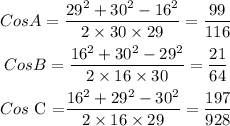
We can then derive the angle as;

Answer: