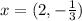Question

Solve using the quadratic FORMULAshow all work3x^2=5x+2

Answer 1

The given quadratic equation is

`3x^2=5x+2`

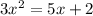
First of all, let us re-write the equation in standard form.

`3x^2-5x-2=0`

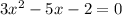
Recall that the standard form of a quadratic equation is given by

`ax^2+bx+c=0`

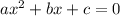
Comparing the standard form with the given equation we see that,

a = 3

b = -5

c = -2

Now we can solve using the quadratic formula.

`x=(-b\pm√(b^2-4ac))/(2a)`

Let us substitute the values of the coefficients a, b, c

`\begin{gathered} x=\frac{-(-5)\pm\sqrt[]{(-5)^2-4(3)(-2)}}{2(3)} \\ x=\frac{5\pm\sqrt[]{25^{}-(-24)}}{6}=\frac{5\pm\sqrt[]{25^{}+24}}{6}=\frac{5\pm\sqrt[]{49}}{6}=(5\pm7)/(6) \end{gathered}`

So, the two possible solutions of the quadratic equation are

`\begin{gathered} x_1=(5+7)/(6)\: \text{and}\: x_2=(5-7)/(6) \\ x_1=(12)/(6)\: \text{and}\: x_2=(-2)/(6) \\ x_1=2\: \text{and}\: x_2=-(1)/(3) \end{gathered}`

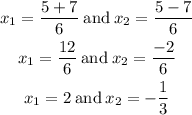
Therefore, the solution of the given quadratic equation is

`x=(2,-(1)/(3))`