Question

The perpendicular bisectors of ABC meet at point G. If BG=27and AG=13+7x, solve for x.

Answer 1

x = 2

Step-by-step explanation:

Given:

BG = 27

AG = 13 + 7x

Note that when three perpendicular bisectors of the sides of a triangle meet at a point, the point is called a Circumcenter.

Also, note that the Circumcenter is equidistant from the vertices of the triangle.

So for the given triangle, G is the circumcenter, and AG = BG = CG.

Let's go ahead and solve for x as seen below;

`\begin{gathered} BG=AG \\ 27=13+7x \end{gathered}`

Let's subtract 13 from both sides of the equation, we'll have;

`\begin{gathered} 27-13=13-13+7x \\ 14=7x \end{gathered}`

Let's divide both sides by 7;

`\begin{gathered} (14)/(7)=(7x)/(7) \\ 2=x \\ \therefore x=2 \end{gathered}`

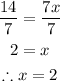
So the value of x is 2