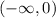Question

Write the answer in interval notation 5(4x+1)<5

Answer 1

We are given the following inequality

`5(4x+1)<5_{}`

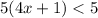
Let us solve the above inequality for x.

Divide both sides of the inequality by 5

`\begin{gathered} (5(4x+1))/(5)<\frac{5_{}}{5} \\ 4x+1<1 \end{gathered}`

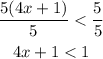
Subtract 1 from both sides of the inequality

`\begin{gathered} 4x+1-1<1-1 \\ 4x<0 \end{gathered}`

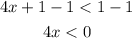
Finally, divide both sides of the inequality by 4

`\begin{gathered} (4x)/(4)<(0)/(4) \\ x<0 \end{gathered}`

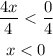
So, the solution is all the values less than 0 (0 is not included in the solution)

The solution in the interval notation is given by

`(-\infty,0)`