Question

Find the number b such that the line y = b divides the region bounded by the curves y = 36x2 and y = 4 into two regions with equal area. (Round your answer to two decimal places.) b =

Answer 1

`b=\sqrt[3]{16}`

Explanation:

Determine interception point of curves

`36x^2=4`

`x^2=(4)/(36)`

`x^2=(1)/(9)`

`x=\pm(1)/(3)`

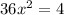
Find the area of the bounded region

`\int\limits^(1)/(3) _{-(1)/(3)} {4-36x^2} \, dx\\ \\=4x-12x^3\Bigr|_{-(1)/(3) }^{(1)/(3) }\\\\=[4((1)/(3))-12((1)/(3))^3]-[4(-(1)/(3))-12(-(1)/(3))^3]\\\\=(8)/(9)-(-(8)/(9))\\\\= (8)/(9)+(8)/(9) \\\\=(16)/(9)`

Therefore, since half of the area is
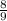`(8)/(9)`, we can set one-half of the region between 0 and x where
`x=(√(b))/(6)` and determine b:

`(8)/(9)=\int\limits^(√(b))/(6) _0 {b-36x^2} \, dx\\\\(8)/(9) =bx-12x^3\Bigr|_(0)^{(√(b))/(6) }\\\\(8)/(9)=b((√(b))/(6))-12((√(b))/(6))^3\\\\(8)/(9)=(b√(b))/(6)-12(\frac{b^{(3)/(2)}}{216})\\\\(8)/(9)=(b√(b))/(6)-(\frac{b^{(3)/(2)}}{18})\\\\(16)/(18)=(3b√(b))/(18)-\frac{b^{(3)/(2)}}{18}\\\\16=3b√(b)-b^{(3)/(2)}\\\\16=3b^{(3)/(2)}-b^{(3)/(2)}\\\\16=2b^{(3)/(2)}`

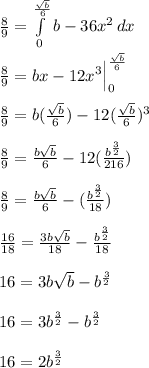
To account for both halves of the region:

`16=2(2b^{(3)/(2)})\\16=4b^{(3)/(2)}\\4=b^{(3)/(2)}\\b=\sqrt[3]{16}`

Therefore, the line
`b=\sqrt[3]{16}` will divide the area between the curves into two regions with equal area