Question

In a right triangle, the acute angles have the relationship sin(2x)=cos(2x-10). What is the value of X?

Answer 1

The given expression is

`\sin (2x)=\cos (2x-10)`

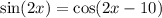
To find the correct value, we just have to evaluate each option.

`\begin{gathered} \sin (2\cdot20)=\cos (2\cdot20-10) \\ \sin 40=\cos 30 \end{gathered}`

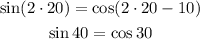
This is not true, so x = 20 is not the solution.

x = 21.

`\begin{gathered} \sin (2\cdot21)=\cos (2\cdot21-10) \\ \sin 42=\cos 32 \end{gathered}`

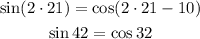
x = 24

`\begin{gathered} \sin (2\cdot24)=\cos (2\cdot24-10) \\ \sin 48=\cos 38 \end{gathered}`

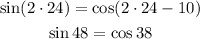
x = 25.

`\begin{gathered} \sin (2\cdot25)=\cos (2\cdot25-10) \\ \sin 50=\cos 40 \\ 0.766\ldots=0.766\ldots \end{gathered}`

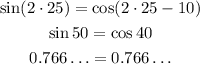
As you can observe, the last option satisfies the equation.

Therefore, option 4 is the answer.